【软考zst2001专辑笔记】004数据结构-下卷

发表于
【软考zst2001专辑笔记】004数据结构-下卷

一、查找

1.1 基本概念

静态查找表：顺序查找、折半（二分）查找、分块查找

动态查找表：二叉排序树、平衡二叉树、B树、哈希表

静态查找表：

  • 查找某个特定的数据元素是否在查找表中。
  • 检索某个特定的数据元素的各个属性。

动态查找表：

  • 在查找表中插入一个数据元素
  • 在查找表中删除一个数据元素

1.2 顺序查找

适用于顺序存储和链式存储。

平均查找长度：n+12 \frac{n+1}{2}

1.3 折半查找

折半查找的必要条件：顺序存储，有序。

最坏的比较次数：⌊log⁡2n⌋+1 \lfloor \log_2 n \rfloor + 1

平均查找长度：log⁡2(n+1)−1 \log_2(n+1) - 1

折半查找过程与关键字比较的次数即为被查找结点在树中的层数。

我自己在这提一下，如果不考虑查找的元素不存在的问题，斐波那契查找更快（基于Java8开发过程中发现的）。

折半查找的比对顺序有以下几种可能：

  1. 大大大大大……（越来越大）
  2. 小小小小小……（越大越小）
  3. 大小大小大……（大小间隔）
  4. 小大小大小……（小大间隔）

二、哈希表

2.1 定义

核心思想是：把查找关键字的值，通过一个函数计算，直接得到它应该存放在哪里。

具有相同哈希数值的关键字，对于该哈西函数来说称为同义词。

2.2 哈希函数构造与处理冲突

哈希函数构造方法：直接定址法、数字分析法、平方取中法、折叠法、随机数法、除留余数法

H(Key) = Key % m = 地址

m取接近n(元素个数)但是大于n的质数。

开放定址法：

  1. 线性探测法：如果该位置已被占用（无论是因为另一个键值对还是之前因冲突而移动至此的键值对），则按顺序检查下一个位置（即 (h(key) + 1) % table_size`）
  2. 二次探测再散列：如果该位置已被占用，则按照二次函数的规律，探测 (h(key) + 1²) % m, (h(key) + 2²) % m, (h(key) + 3²) % m`, …，直到找到一个空位置为止。
  3. 随机探测再散列：如果位置被占用，则使用一个伪随机数生成器（PRNG）来决定下一个探测的位置。这个生成器的种子通常与当前的 key 相关，以确保对于同一个 key，探测序列是确定且可重现的。

2.3 处理冲突拓展和装填因子

链地址法：

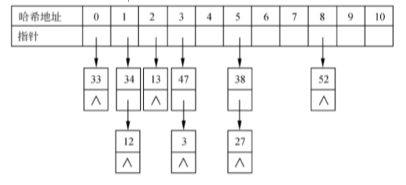
哈希表的填装因子定义为：α = 表中装入的记录数哈希表的长度 \frac{表中装入的记录数}{哈希表的长度}

α越小，发生冲突的可能性越小。

三、排序

排序算法 平均时间复杂度 最坏时间复杂度 最好时间复杂度 空间复杂度 稳定性
快速排序 O(nlg⁡n n \lg n ) O(n2) O(nlg⁡n n \lg n ) O(nlg⁡n n\lg n ) 不稳定
归并排序 O(nlog⁡2n n \log_2 n ) O(nlog⁡2n n \log_2 n ) O(nlog⁡2n n \log_2 n ) O(n) 稳定
直接插入排序 O(n2) O(n2) O(n) O(1) 稳定
简单选择排序 O(n2) O(n2) O(n2) O(1) 不稳定
冒泡排序 O(n2) O(n2) O(n) O(1) 稳定
堆排序 O(nlog⁡2n n \log_2 n ) O(nlog⁡2n n \log_2 n ) O(nlog⁡2n n \log_2 n ) O(1) 不稳定
希尔排序 O(n1.3) O(n2) O(n) O(1) 不稳定

3.1 直接插入排序

🌰：你手里有一副乱序的牌，现在你要把它们从小到大排好。你从左到右一张一张看：

  1. 第一张牌，不用排，自己就是“有序”的。
  2. 拿第二张牌，跟第一张比一下，小就插到前面，大就放后面。现在前两张是有序的。
  3. 拿第三张牌，从右往左一个个比，把它插到正确的位置，让前三张有序。
  4. 继续这样，每拿一张新牌，都把它插入到前面已排序部分的正确位置。

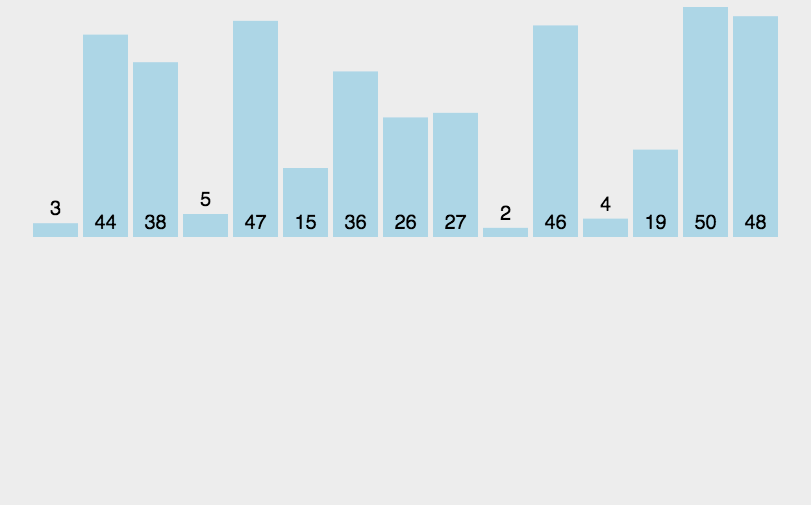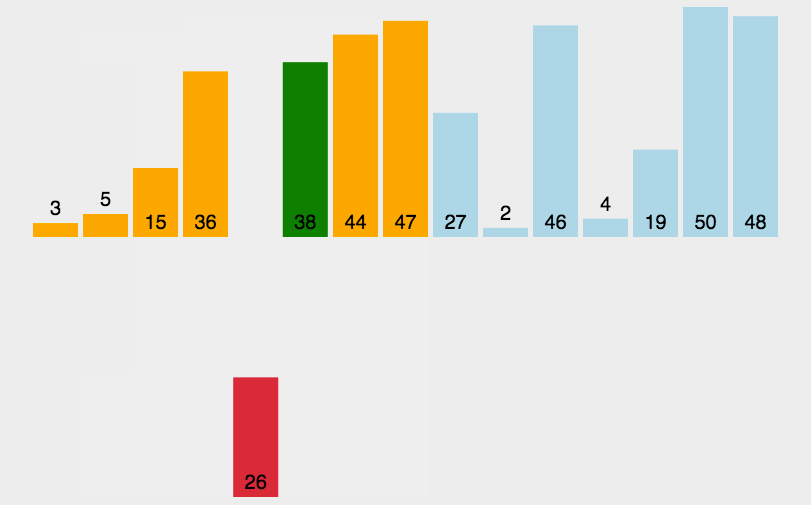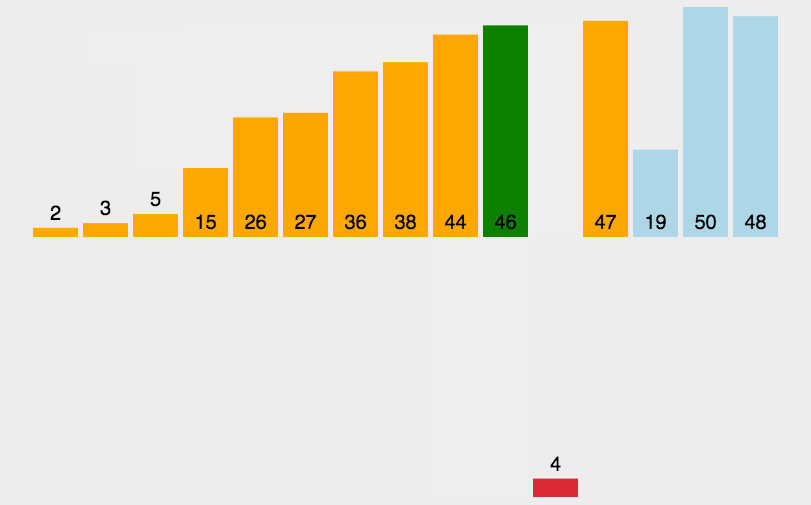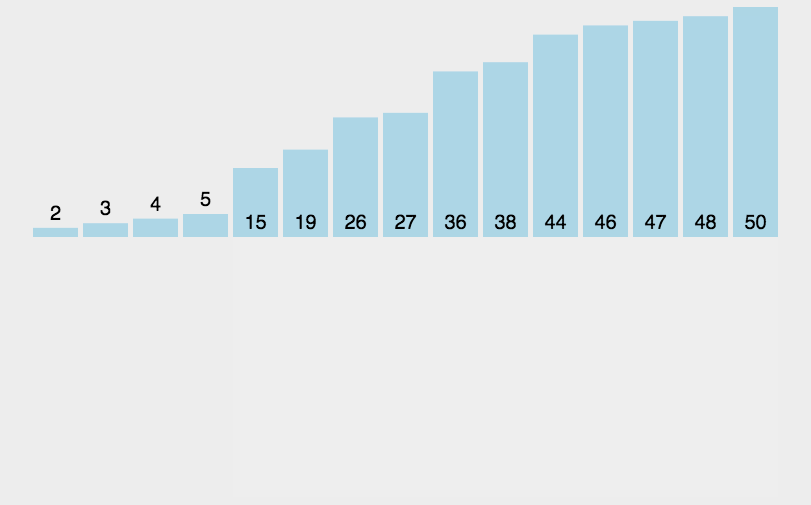
3.2 希尔排序

🌰：整理书架上的书（按高度排序）：

  1. 先每隔几本排一次（大间隔）比如每隔 4 本书为一组
  2. 缩小间隔，比如每隔 2 本一组
  3. 最后，间隔为1，做一次普通插入排序

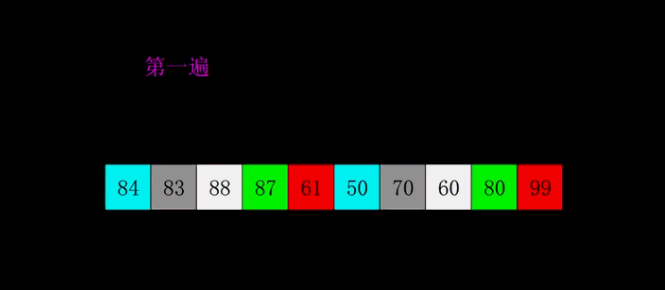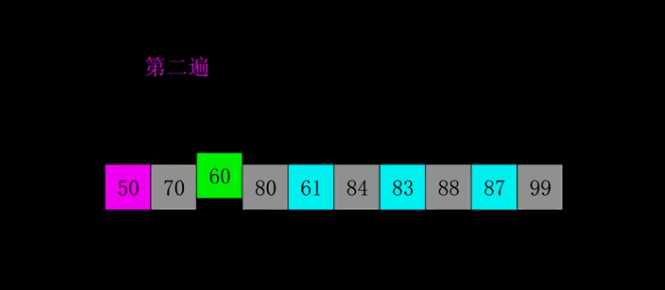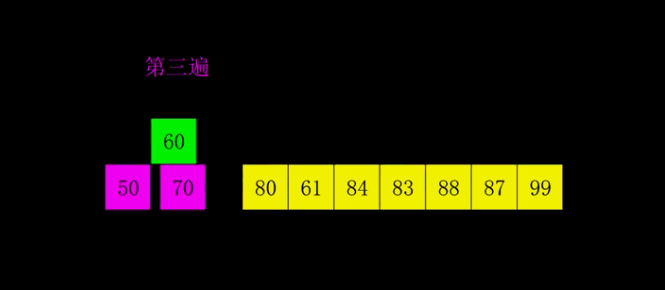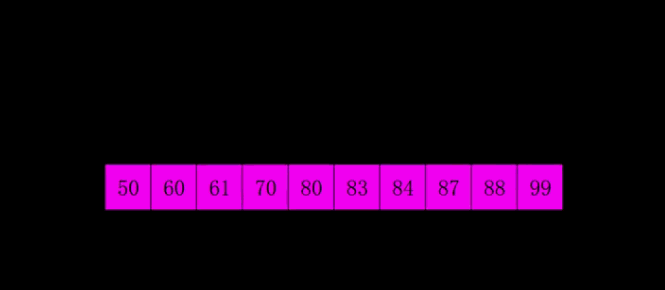
3.3 计数排序

假设你有一堆小朋友的年龄，范围是 0 到 5 岁，想把他们按年龄从小到大排序。

  1. 数一数每个年龄有多少人，拿一个表格（数组），从 0 开始，数每个年龄出现的次数：
  2. 按顺序把年龄写出来。从年龄 0 开始，写 1 个 0，写 2 个 1，写 1 个 2，写 2 个 3……以此类推。

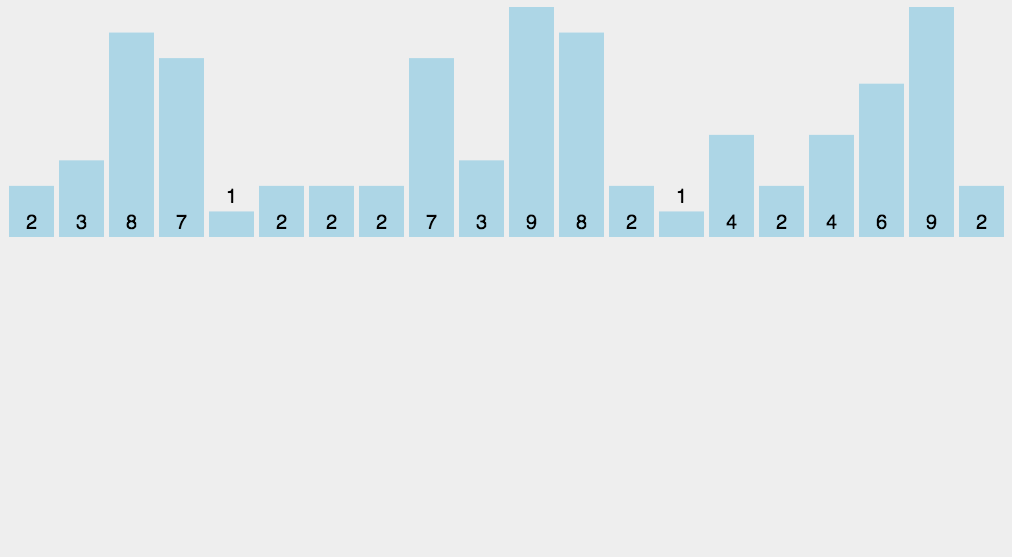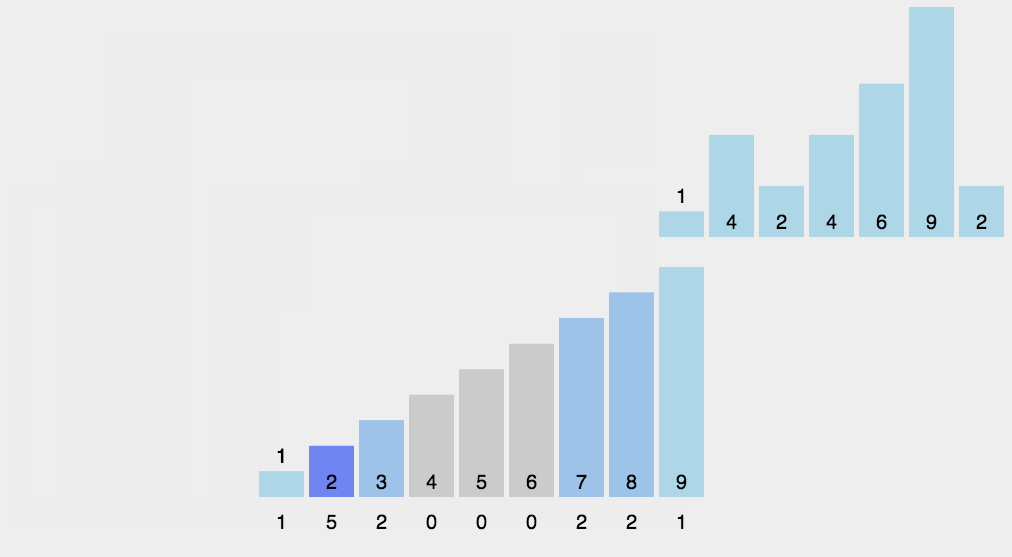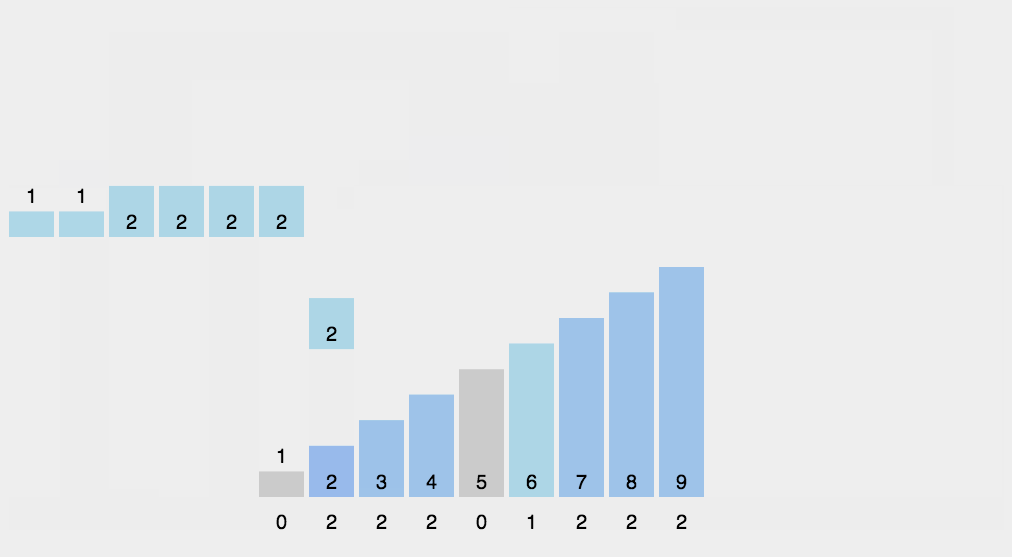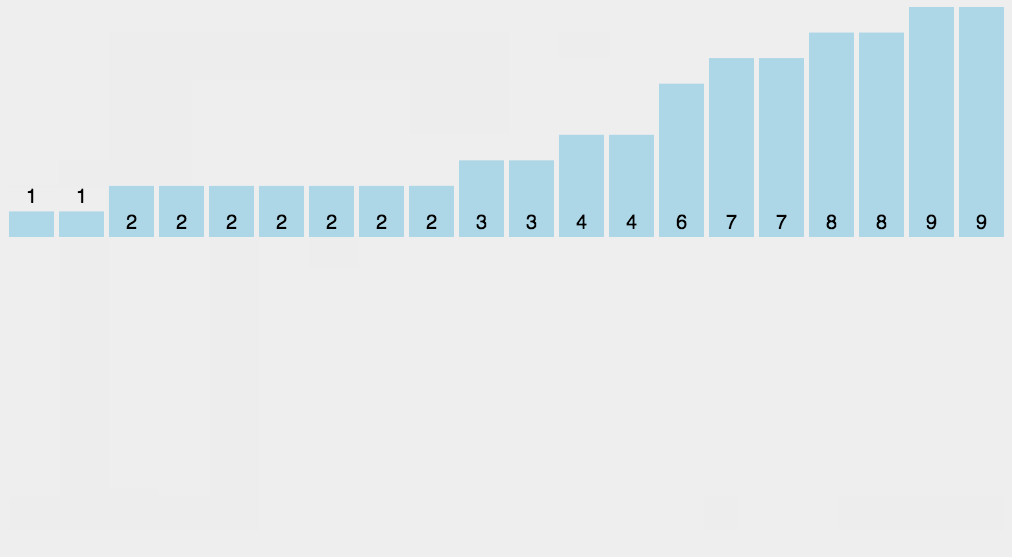
3.4 简单选择排序

每次从剩下的数里，挑出最小的那个，放到前面。

  1. 在所有数 [5, 2, 4, 1, 3] 中找最小的
  2. 在剩下的 [2, 4, 5, 3]` 中找最小的
  3. 在剩下的 [4, 5, 3]` 中找最小的
  4. 在剩下的 [5, 4]` 中找最小的

3.5 堆排序

  1. 建立大顶堆
  2. 将大的权值向后排（重复此步骤）

3.6 冒泡排序

一排站在一起的高矮不一的学生（比如5个人），把他们按照从矮到高的顺序重新排列。

  1. 从最左边开始：让第1个和第2个学生比身高。 如果左边（第1个）比右边（第2个）高，就让他们交换位置（让高的去右边）。
  2. 向右移动：接着让第2个和第3个学生比身高，同样，如果左边的比右边高就交换。
  3. 一直比到最后：继续这个过程，一直比到最后一对（第4个和第5个学生），最高的那个学生一定会被排到最右边
  4. 重复这个过程：现在，最高的学生已经就位了。我们忽略最后一个位置（因为他已经排好了）。

img

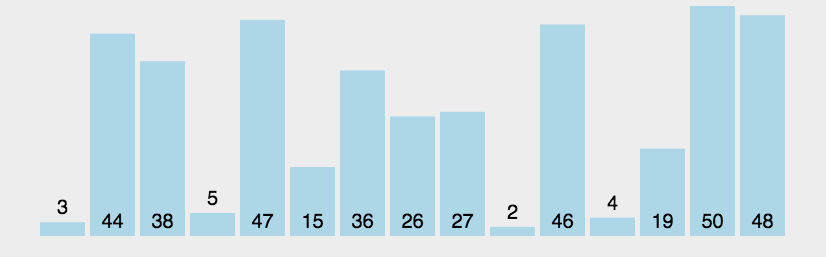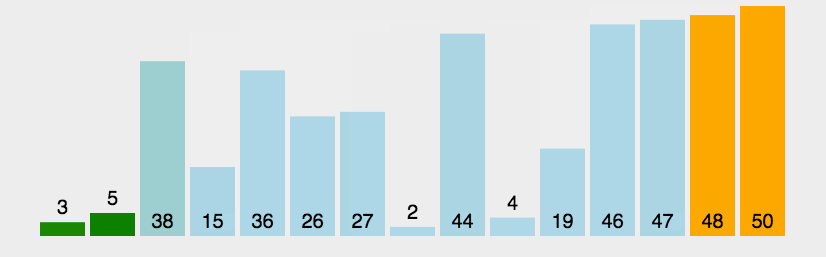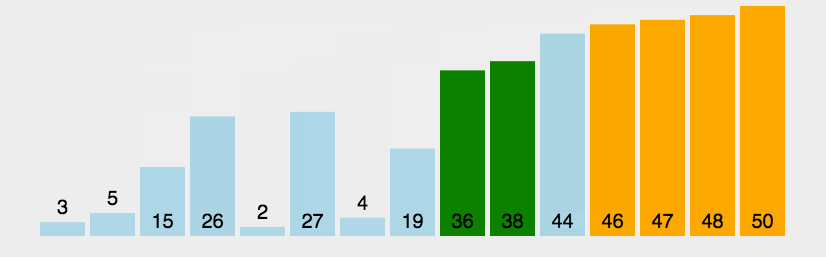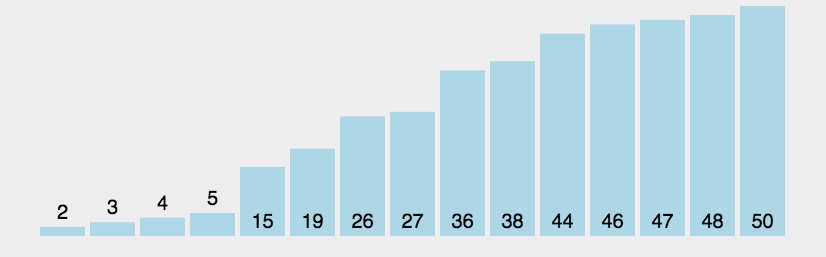
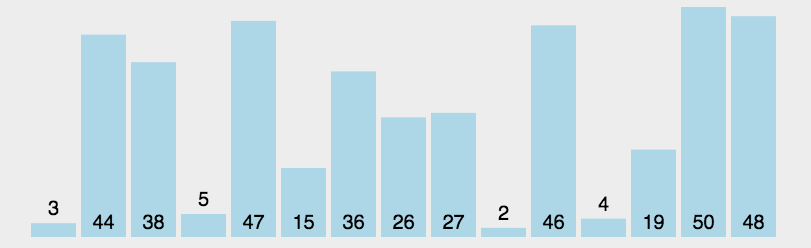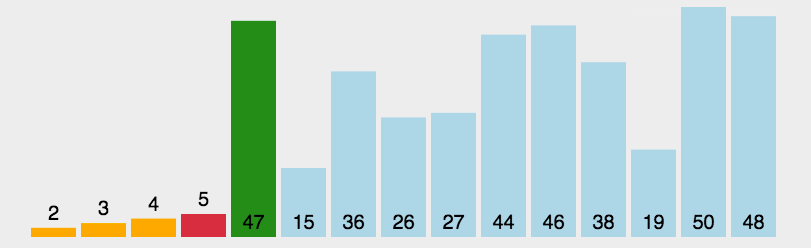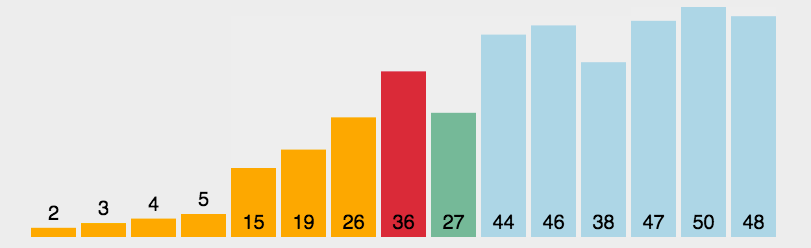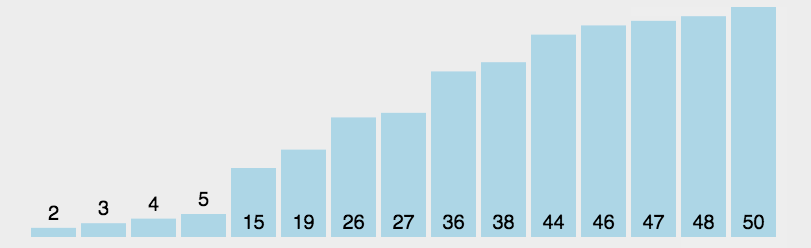
3.7 快速排序

想象你有一堆杂乱无章的书，你需要把它们按照高度从矮到高排列。

  1. 挑一本“标杆”书：从书堆里随便拿起一本书（比如正中间那本），这本书的高度就是我们的“标杆”。

  2. 分区操作（核心！）：现在，你开始整理剩下的书：

    • 创建一个 “矮个子区”（左边），创建一个 “高个子区”（右边）

    • 然后，你一本一本地拿起剩下的书，和手里的“标杆”书比身高：如果比“标杆”矮，就扔到 “矮个子区”。如果比“标杆”高，就扔到 “高个子区”。

  3. 递归排序：现在你有了三堆书：

    • 左边的一堆 “矮个子”（它们都比标杆矮，但内部顺序是乱的）
    • 中间的一本“标杆”（它现在已经在了最终正确的位置上！）
    • 右边的一堆 “高个子”（它们都比标杆高，但内部顺序也是乱的）右边的一堆 “高个子”（它们都比标杆高，但内部顺序也是乱的）

  4. 对左右两堆重复：对左边的“矮个子区”和右边的“高个子区”分别重复步骤1-3（再为它们选新的“标杆”，再分区）。

  5. 合并：当每一堆小书堆都只剩下0本或1本书时（0或1本书本身就有序，不需要再排），把所有排好序的小书堆从左到右（矮区 + 标杆 + 高区）合并起来，整个序列就有序了。

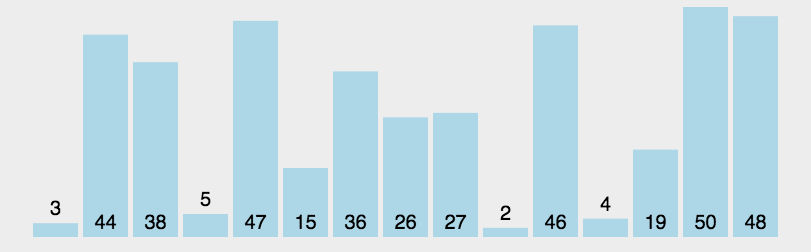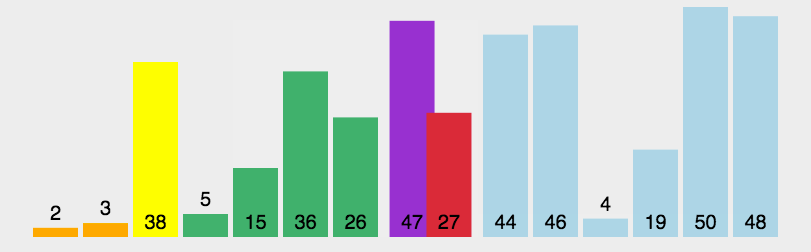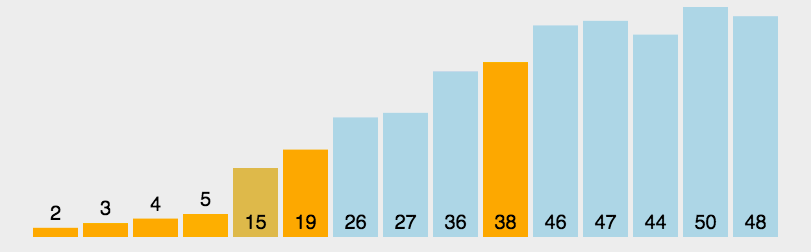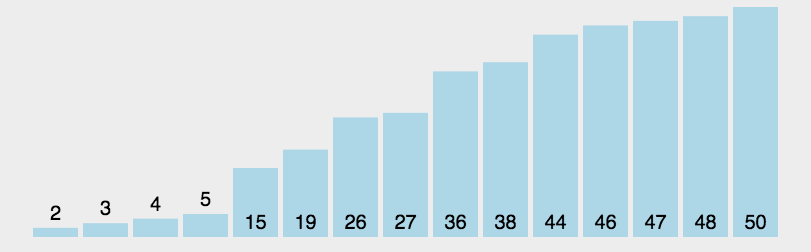
3.8 归并排序

有两叠已经按从小到大排好序的扑克牌（比如一叠是[3, 8, Q]，另一叠是[5, 9, K]），合并成一叠新的有序牌。

  1. 总是比较最上面的牌：你看两叠牌最上面的一张，左边是3，右边是5。
  2. 拿出小的那张：3比5小，所以你拿出左边的3，放到新牌堆里。
  3. 继续比较：现在左边最上面是8，右边还是5。5比8小，所以你拿出右边的5，放到新牌堆（现在是[3, 5]）。
  4. 重复直到完：继续这个过程（比较8和9，拿8；比较Q和9，拿9；最后把Q和K依次拿出）。
  5. 最终：你得到了一个全新的、有序的牌堆：[3, 5, 8, 9, Q, K]。

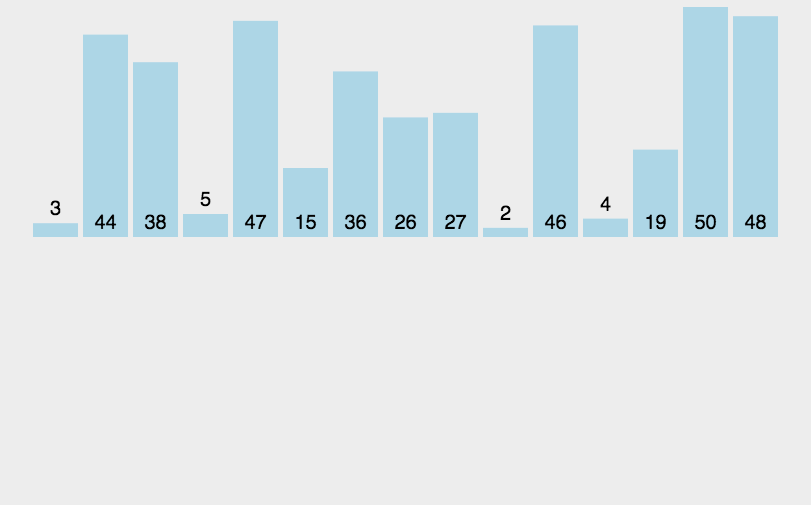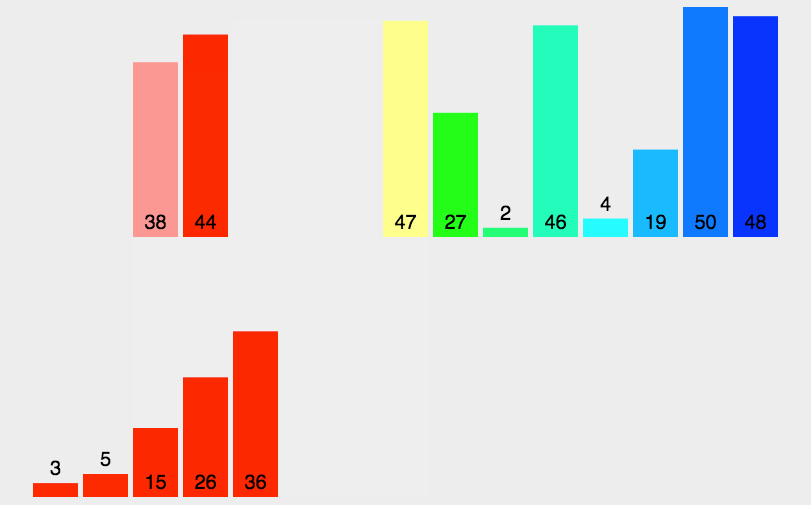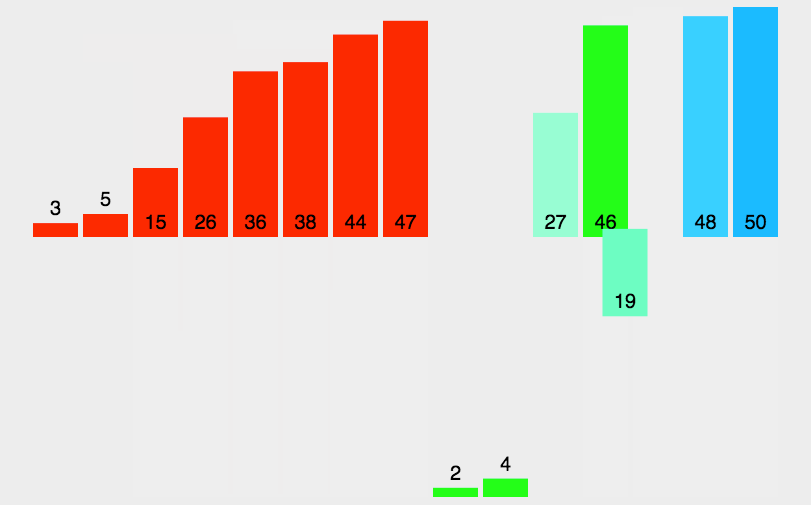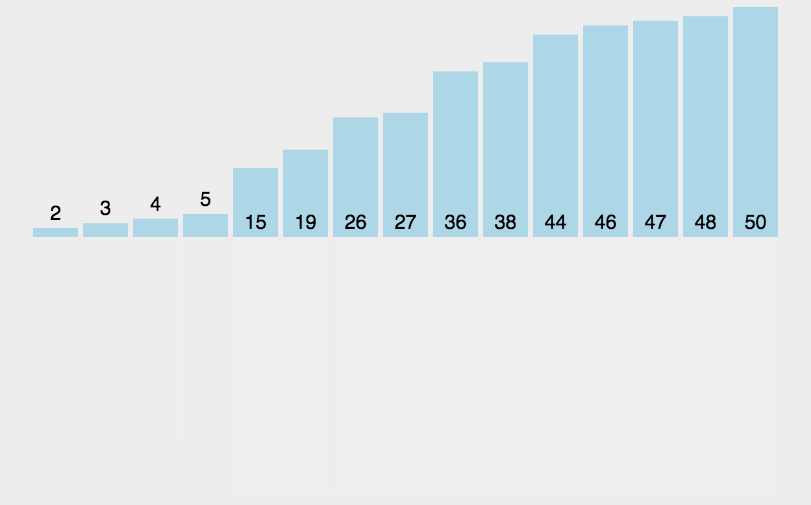
3.9 排序算法总结

排序算法 核心思想 关键字 大概的逻辑
快速排序 分区、递归 基准、分区 一分为二，递归下去。
归并排序 先分后合、递归 分治、合并 先分后合，分治典范。
堆排序 利用堆结构 建堆、取顶 建堆取顶，反复调整。
希尔排序 分组插入 间隔、分组 分组插入，由粗到细。
直接插入排序 插牌 插入、有序序列 摸牌插牌，步步为营。
冒泡排序 两两交换 相邻比较、交换 两两比较，大的下沉。
简单选择排序 选择最值 选择、最值 每次选最小，放到最前面。
  • 带“递归/分治”的：快排、归并。
  • 带“插入”的：直接插入（基础）、希尔（改进版）。
  • 名字即方法：选择、冒泡。
  • 用数据结构的：堆排序。