【软考zst2001专辑笔记】003数据结构-上卷
一、大O表示法
算法时间复杂度:以算法中基本操作重复执行的次数(简称频度)作为算法的时间度量。
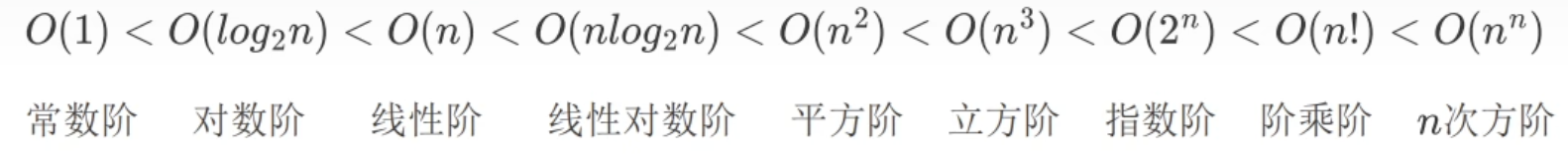
加法规则:多项相加,保留最高阶项,并将系数化为1
乘法法则:多项相乘都保留,系数化为1
加法乘法混合规则:先小括号 再乘法规则 最后加法规则
二、时间复杂度
例子:
- O(1):
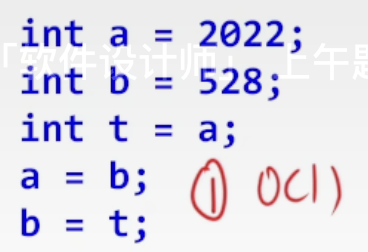
- O(log2n):

- O(n):

- O(nlog2n):

- O(n2):

- O(n3):

三、空间复杂度
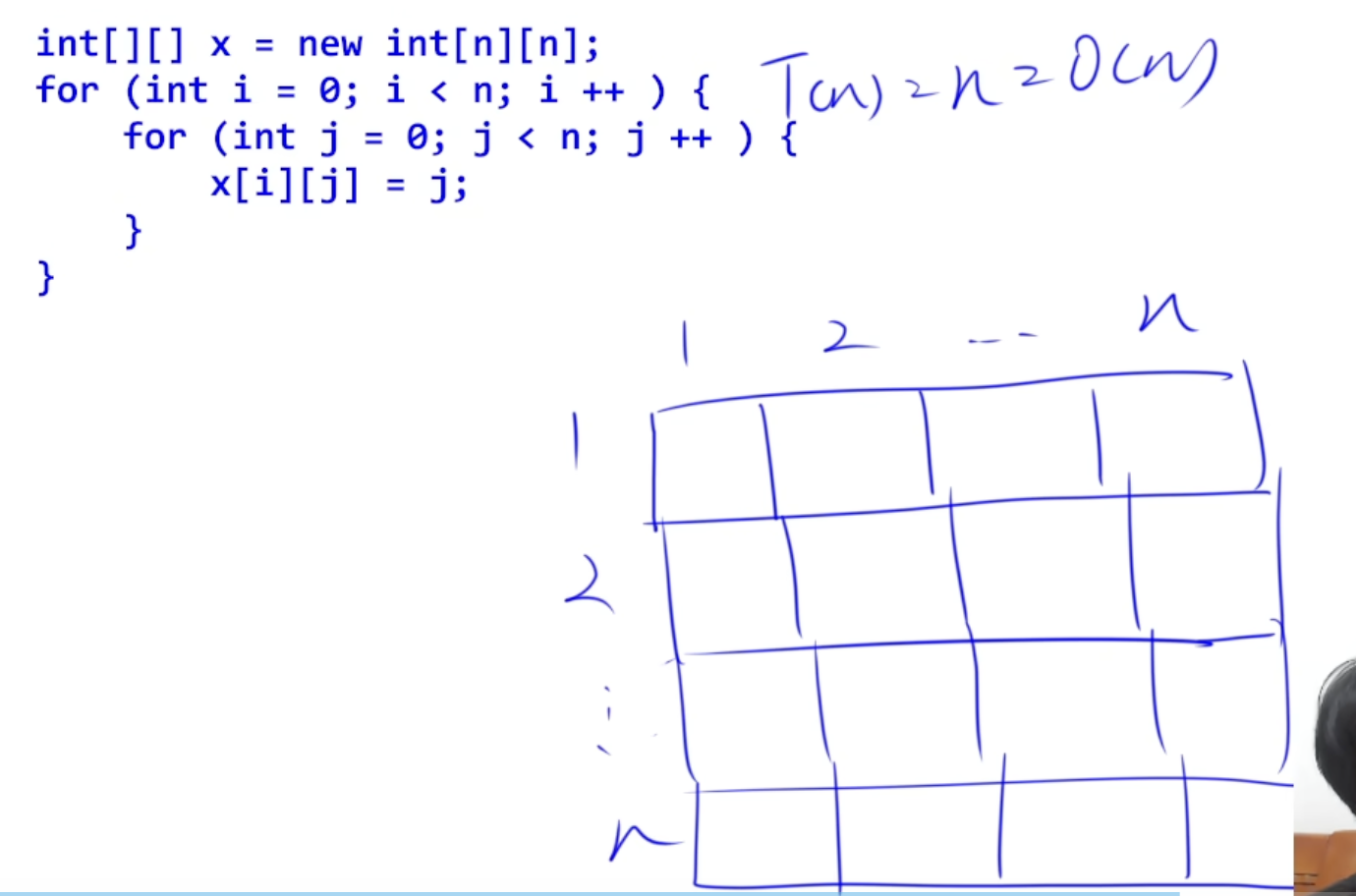
T(n) = n2 = O(n2)
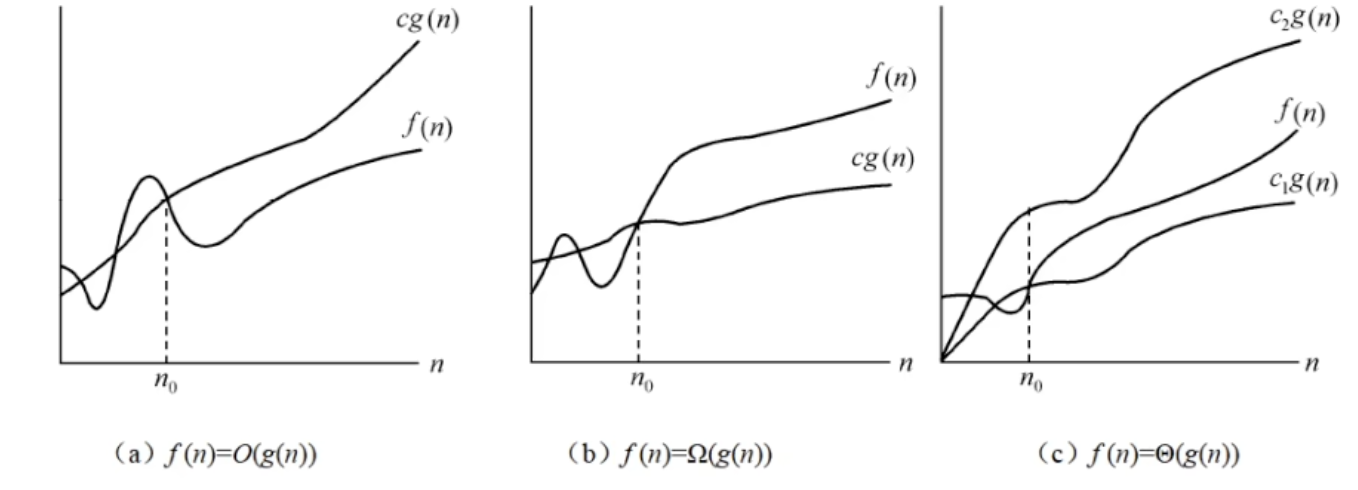
四、渐进符号
- 渐进上界
- 符号:
O - 含义:
f(n)的增长速度至多与g(n)一样快(或更慢)。它给出了函数f(n)的一个上界。常用于描述算法的最坏情况时间复杂度。 - 类比:
f(n) ≤ g(n)(在渐进意义上)。
- 符号:
- 渐进下界
- 符号:
Ω - 含义:
f(n)的增长速度至少与g(n)一样快(或更快)。它给出了函数f(n)的一个下界。常用于描述算法的最好情况时间复杂度。 - 类比:
f(n) ≥ g(n)(在渐进意义上)。
- 符号:
- **渐进紧致界 **
- 符号:
Θ - 含义:
f(n)的增长速度精确地与g(n)一样快。它同时是f(n)的上界和下界,因此是一个紧致界。当算法的最好情况和最坏情况复杂度相同时,常用Θ来描述其平均情况或精确的时间复杂度。 - 类比:
f(n) = g(n)(在渐进意义上)。
- 符号:
五、递归式时间、空间复杂度
时间复杂度 = 递归的次数 x 每次的时间复杂度 (每次递归时间复杂度不变的情况下)
空间复杂度 = ????
这一章讲的不是很清晰,学的也不是很透彻,待定吧
六、递归式主方法
T(n) = aT(n/b) + f(n)
例子:
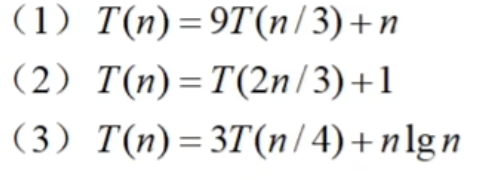
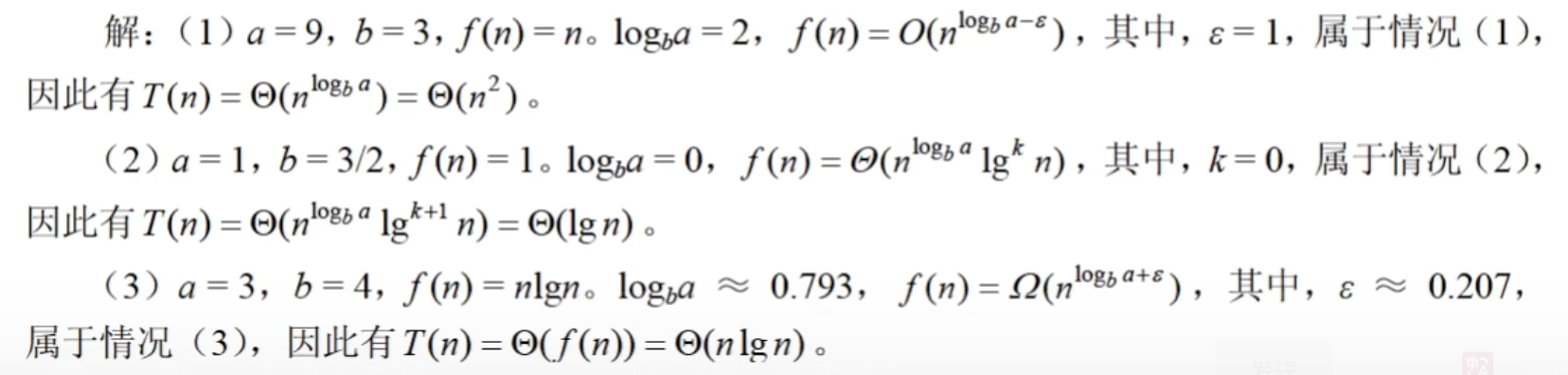
七、线性结构与线性表定义
特点:数据元素之间呈现一种线性关系,即元素“一个接一个排列”。
线性表:顺序存储、链式存储。
非空线性表特点:
- 存在唯一的一个称为“第一个”的元素。
- 存在唯一的一个称为“最后一个”的元素。
- 除第一个元素外,序列中的每个元素均只有一个直接前驱
- 除最后一个元素外,序列中的每个元素均只有一个直接后继。
7.1 线性表的顺序存储
顺序存储是指,一组地址连续的存储单元依次存储线性表中的数据元素。
优点:可以随机存取表中元素。
缺点:插入、删除都需要移动元素。
插入一个新元素需要移动的元素个数期望值为:n/2
删除元素时需要移动的元素个数期望值为:(n-1)/2
7.2 顺序表的插入、删除、查找时间复杂度
| 插入时间复杂度 | |
|---|---|
| 最好 | O(1) |
| 最坏 | O(n) |
| 平均 | O(n) |
| 删除时间复杂度 | |
|---|---|
| 最好 | O(1) |
| 最坏 | O(n) |
| 平均 | O(n) |
| 查找时间复杂度 | |
|---|---|
| 最好 | O(1) |
| 最坏 | |
| 平均 |
7.3 顺序表的链式存储

数据域用于存储元素的值,指针域用于存储元素的直接前驱或直接后继的位置信息。
各个数据元素的节点的地址并不要求是连续,因此存储数据元素的同时,必须存储元素的逻辑关系。
若元素的结点只有一个指针域,称为线性链表(单链表)

7.4 单链表的插入、删除、查找时间复杂度
| 插入时间复杂度 | |
|---|---|
| 最好 | O(1) |
| 最坏 | O(n) |
| 平均 | O(n) |
| 删除时间复杂度 | |
|---|---|
| 最好 | O(1) |
| 最坏 | O(n) |
| 平均 | O(n) |
| 查找时间复杂度 | |
|---|---|
| 最好 | O(1) |
| 最坏 | O(n) |
| 平均 | O(n) |
7.5 循环单链表、双链表
循环单链表:尾结点的指针域指向头结点。
双链表:两个指针域,分别指向前驱和后继。
八、栈相关
8.1 栈的顺序存储
先进后出
基本运算:
- 初始化栈:创建一个空栈
- 判栈空:当栈为空时返回真,否则返回假
- 入栈:将元素x加入栈顶,并更新栈顶指针
- 出栈:将元素从栈中删除,并更新栈顶指针。
- 读站定元素:返回栈顶元素的值,但不修改栈顶指针
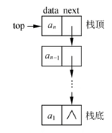
8.2 栈的链式存储
九、队列相关
9.1 队列的顺序存储与循环队列
先进先出。允许插入元素的一端为队尾,允许删除元素的一段为队头。
由于队列的元素插入和删除分别再两端进行,因此设置队头指针和队尾指针。
运算:
- 初始化队列:创建一个空的队列。
- 判队空:当队列为空时返回真,否则返回假。
- 入队:将元素加入到队列的队尾,并更新队尾指针。
- 出队:将队头元素从队列中删除,并更新队头指针。
- 读队头元素:返回队头元素的值,但不修改队头指针。
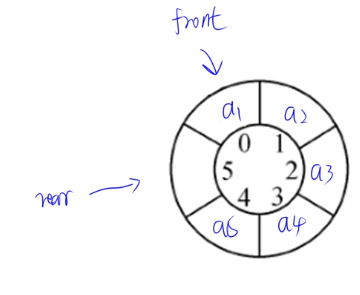 循环队列
循环队列
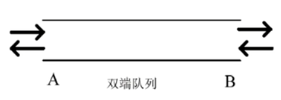
9.2 队列的链式存储与双端队列
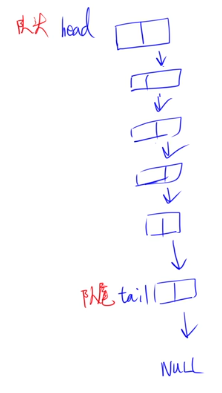 队列的链式存储
队列的链式存储

十、串相关
特殊的线性表,元素为字符。
基本概念:
- 空串:长度为零称为空串,空串不包含任何字符。
- 空格串:由一个或多个空格组成的串。空格在计算长度是也要将其计算在内。
- 子串:串中任意长度的连续字符构成的序列称为子串。空串是任意串的子串。
- 串相等:两个串长度相等,且对应序号的字符相同。
- 串比较:比较两个串大小时,以字符的ASCII码作为依据。
10.1 串的模式匹配与朴素模式匹配
最好:O(m)
最坏:O(nm)
平均:O(n+m)
10.2 手算next数组值
串的前缀:包含第一个字符并且不包含最后一个字符的子串
串的后缀:包含最后一个字符并且不包含第一个字符的子串
第i个字符的next值 = 从1 ~ i-1 串中最长相等前后缀长度 + 1
特殊情况:next[1] = 0
**手算步骤(以模式串 **ABABC 为例)
模式串:P = "ABABC"
我们逐位计算 next[i]:
- i = 0: 子串
A
- 没有真前后缀 →
next[0] = 0
- i = 1: 子串
AB
- 前缀:
A - 后缀:
"B" - 无相等前后缀 →
next[1] = 0
- i = 2: 子串
ABA
- 前缀:
"A","AB" - 后缀:
"A","BA" - 相等的有:
"A"(长度1) - 最长相等真前后缀长度 = 1 →
next[2] = 1
- i = 3: 子串
ABAB
- 前缀:
"A","AB","ABA" - 后缀:
"B","AB","BAB" - 相等的有:
"AB"(长度2) - 最长 = 2 →
next[3] = 2
- i = 4: 子串
ABABC
- 前缀:
"A","AB","ABA","ABAB" - 后缀:
"C","BC","ABC","BABC" - 没有相等的前后缀 →
next[4] = 0
✅ 最终next数组:
| i | P[i] | 子串 | next[i] |
|---|---|---|---|
| 0 | A | A | 0 |
| 1 | B | AB | 0 |
| 2 | A | ABA | 1 |
| 3 | B | ABAB | 2 |
| 4 | C | ABABC | 0 |
👉 所以:next = [0, 0, 1, 2, 0]
✅总结:手算next数组口诀
逐位看子串,拆分前和后,
找最长相等,记长度为next。
单字符为0,无匹配也为0,
前后缀不重叠,才是“真”前后。
十一、数组相关
11.1 一维数组
L:元素大小
LOC:数组首地址
内存中:a[0] a[1] a[2] a[3] a[4] a[5]
某个元素在内存中实际地址的公式:
下标从0开始: ai = LOC + i x L
下标从1开始: ai = LOC + (i-1) x L
11.2 二维数组
N:行 M:列
L:元素大小
LOC:数组首地址
a[0][0] a[0][1] a[0][2]
a[1][0] a[1][1] a[1][2]
按行优先:a[0][0] a[0][1] a[0][2] a[1][0] a[1][1] a[1][2]
按列优先:a[0][0] a[1][0] a[0][1] a[1][1] a[0][2] a[1][2]
某个元素在内存中实际地址的公式:
按行优先存储,下标从0开始:ai,j =LOC + (i x M + j) x L
按行优先存储,下标从1开始:ai,j =LOC + [(i - 1) x M + (j - 1)] x L
按列优先存储,下标从0开始:ai,j =LOC + (j x N + i) x L
按列优先存储,下标从1开始:ai,j =LOC + [(j - 1) x M + (i - 1)] x L
十二、矩阵相关
12.1 对称矩阵
1 2 3 A0,0 A0,1 A0,3
2 3 4 A1,0 A1,1 A1,3
3 4 5 A2,0 A2,1 A2,3
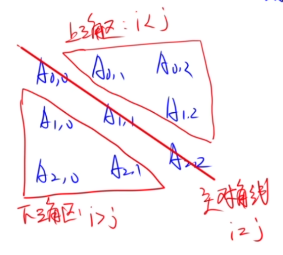 Ai,j = Aj,i
Ai,j = Aj,i
左下三角区 + 主对角线
对称矩阵按行存储下三角区和主对角线并且下标从0(A0.0)开始
当(i ≥ j)时:Ai,j =
当(i ≤ j)时:Ai,j =
对称矩阵按行存储下三角区和主对角线并且下标从1(A1.1)开始
当(i ≥ j)时:Ai,j =
当(i ≤ j)时:Ai,j =
12.2 三对角矩阵
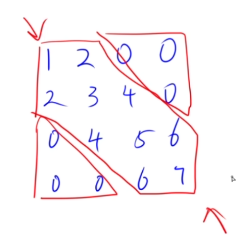
三对角矩阵按行存储并且下标从0(A0,0)开始:Ai,j = 2i + j + 1
三对角矩阵按列存储并且下标从1(A1,1)开始:Ai,j = 2i + j - 2
12.3 稀疏矩阵
顺序存储:三元组顺序表
链式存储:十字链表
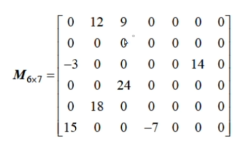
| 行 | 列 | 值 |
|---|---|---|
| 同行的下一个元素 | 同列的下一个元素 |
十三、树相关
13.1属性结构与树的定义
非线性结构
树是n(n≥0)个结点的有限集合,n=0时称为空树。
有且仅有一个结点称为根。
树的定义是递归的,由若干颗子树构成,子树又由更小的子树构成。
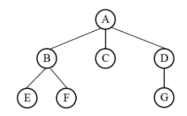
13.2 树的基本概念
- 双亲、孩子:结点的子树称为该节点的孩子,该节点是子结点的双亲。
- 兄弟:具有相同双亲的结点互为兄弟。
- 结点的度:结点的子树的个数。
- 叶子结点:终端结点,度为0的结点。
- 内部结点:也称为分支节点或非终端结点。度不为0,除了根节点外,分支结点也称为内部结点。
- 结点的层次:根为第一层,根的孩子为第二层,以此类推。
- 树的高度(深度):树的最大层次。
13.3 树的性质
- 树的结点总数 = 树所有结点的度数之和 + 1
- 度为m的树中第i层,最多有mi-1个结点(i ≥ 1)
- 高度为h的m次树,最多有
- 具有n个结点、度为m的树,最小高度为(上取整)
13.4 二叉树的定义
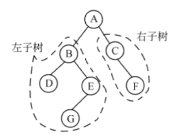
二叉树结点的子树,要区分左子树和右子树。(即使结点只有一棵树的时候也要明确指出)
二叉树的结点最大的度为2
13.5 二叉树的性质
- 二叉树第i层(i ≥ 1)上最多有2i-1个结点
- 高度为h的二叉树最多有2h-1个结点
- 对于任何一棵二叉树,度为0的结点数等于度为2的结点数+1
- 具有n个结点的完全二叉树的高度为或
13.6 满二叉树与完全二叉树
满二叉树:深度为k的二叉树,有2k-1个结点。叶结点只能出现在最底层,且非叶结点的度都为2
完全二叉树:从根到最后一层从左到右依次填满的结构。
满二叉树是完全二叉树的一个特例。
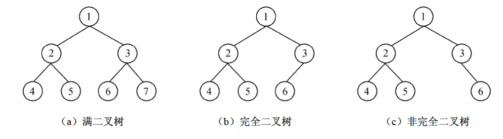
13.7 二叉树顺序存储
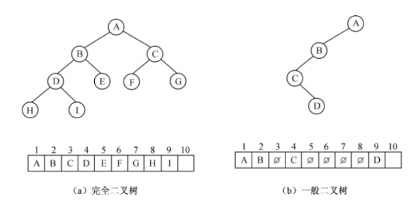
编号为i的结点:i=1,该节点为根节点,无双亲;i>1,则该结点的双亲结点为
完全二叉树适合使用顺序存储,一般二叉树不宜采用顺序存储。
最坏的情况下,一个深度为k且只有k个结点的二叉树(单支树)需要2k-1个存储单元
13.8 二叉树链式存储
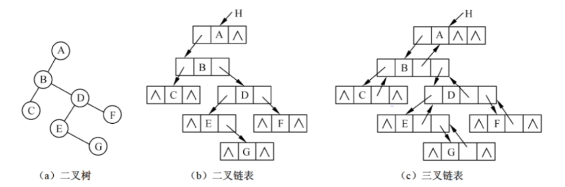
二叉链表:n个节点,有n+1个空指针域
三叉链表:n个节点,有n+2个空指针域
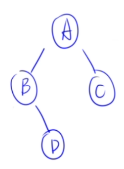
13.9 二叉树遍历
- 先序遍历:根左右
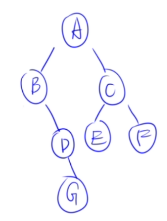
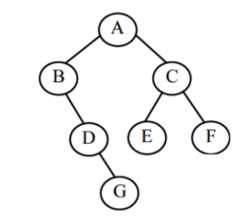 ===> 遍历结果:ABDGCEF
===> 遍历结果:ABDGCEF
- 中序遍历:左根右
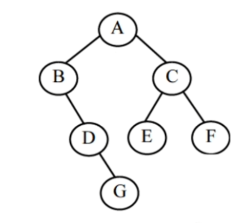 ===> 遍历结果:BDGAECF
===> 遍历结果:BDGAECF
- 后续遍历:左右根
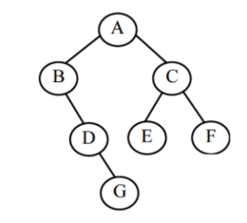 ===> 遍历结果:GDBEFCA
===> 遍历结果:GDBEFCA
- 层序遍历:一层一层,从左到右
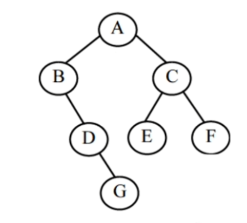 ===> 遍历结果:ABCDEFG
===> 遍历结果:ABCDEFG
13.10 根据遍历构造二叉树
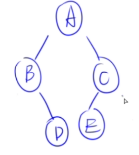
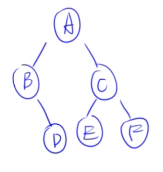
先序遍历:ABDGCEF
中序遍历:BDGAECF
后续遍历:GDBEFCA
层次遍历:ABCDEFG
以上加粗的为根节点,可以从先序、后序、层次中找到。
先序、后序是确定根的位置,中序确定根的子结点。
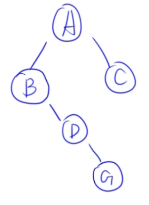
🌰****例子1:
- 先序:ABDGCEF
- 中序:BDGAECF

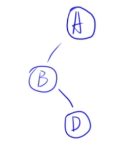
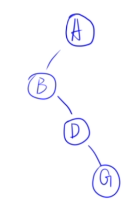
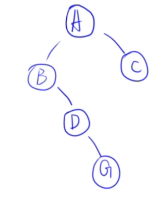
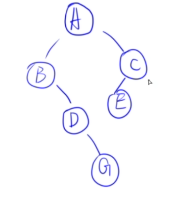
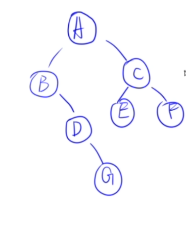
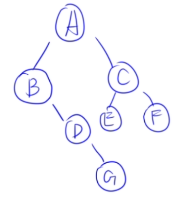
🌰****例子2:
- 后序:GDBEFCA
- 中序:BDGAECF

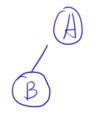
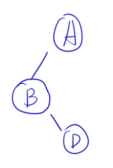
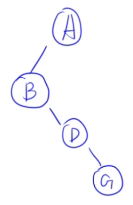
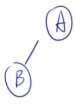
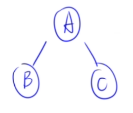
🌰例子3:
- 层次遍历:ABCDEFG
- **中序:**BDGAECF

| 组合 | 是否可构造 | 关键技巧 |
|---|---|---|
| 先序 + 中序 | ✅ | 先序定根,中序分左右,递归 |
| 后序 + 中序 | ✅ | 后序定根,中序分左右,递归 |
| 层序 + 中序 | ✅(较难) | 层序取根,中序分左右,筛选子序列 |
| 其他组合 | ❌ 或不唯一 | 缺少左右子树划分依据 |
13.11 平衡二叉树
二叉树中的任意一个结点的左右子树高度之差的绝对值不超过1
叶子结点满足平衡二叉树的条件要求
完全二叉树是平衡二叉树
13.12 二叉排序树的定义
根节点的关键字 > 左子树所有结点的关键字,
根节点的关键字 **< **右子树所有结点的关键字,
左右子树也是一颗二叉排序树
中序遍历得到的序列是有序序列。
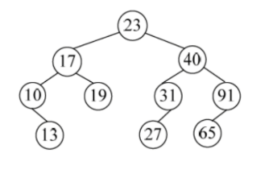
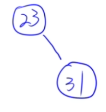
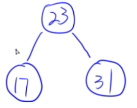
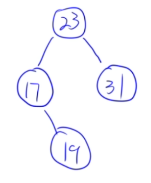
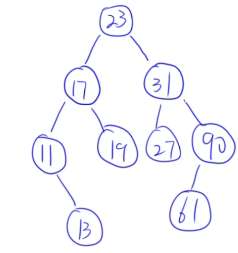
13.13 二叉排序树的构造
例子:
23 31 17 19 11 27 13 90 61

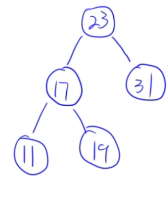
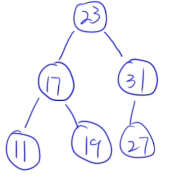
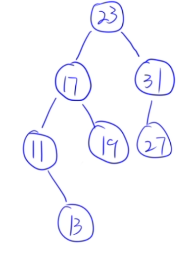
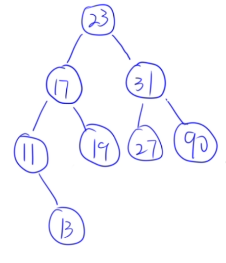
13.14 最优二叉树(哈夫曼树)定义和概念
带权路径长度最短的树。
路径:一个结点到另一个结点之间的通路。
路径上的分支数目称为路径长度。
树的带权路径长度:所有叶子结点的带权路径长度之和,计为WPL
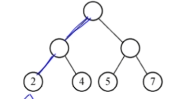 WPL = 2x2 + 4x2 + 5x2 + 7x2 = 36
WPL = 2x2 + 4x2 + 5x2 + 7x2 = 36
被乘数:是叶子结点的关键字
乘数:是根结点到该叶子结点的路径长度。这里从图中可以看出全是2
最优二叉树(哈夫曼树)的三个核心性质:
- 给定一组具有确定权值的叶子结点,构造出的二叉树中带权路径长度(WPL)最小。
- 只有度为0或2,没有度为1
- 总结点数为:2n-1
13.15 最优二叉树构造
最优二叉树不唯一,但是WPL是唯一的。
构造规则:
- 从前往后找2个权值最小
- 小的在左边,大的在右边
- 计算出权值,放入数组末尾
- 权值相同时从前往后
- 回调第一步。
🌰例子:{18、32、4、8、12、26}
- 选4和8。
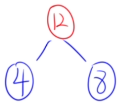
- 选12和12。
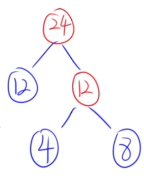
- 选18和24。
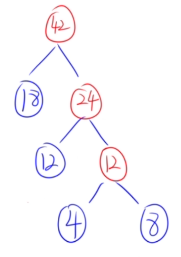
- 选32和26。
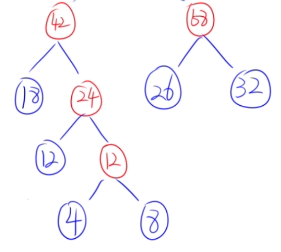
- 合并
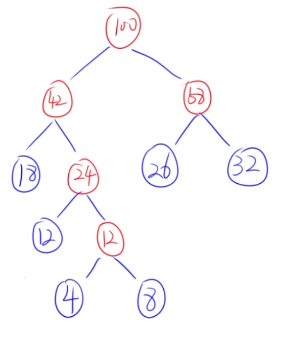
13.16 哈夫曼编码定义
等长编码:对每个字符编值相同长度的二进制编码。
哈夫曼编码:一种根据字符出现频率构建最优前缀码的变长编码技术,用于数据压缩。
| a:45 b:13 c:12 d:16 e:9 f:5 |
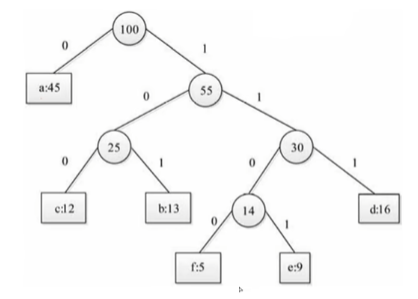 |
a:0 b:101 c:100 d:111 e:1101 f:1100 |
|---|
13.17 哈夫曼编码压缩比.
| 字符 | a | b | c | d | e |
|---|---|---|---|---|---|
| 频率(%) | 40 | 10 | 20 | 16 | 14 |
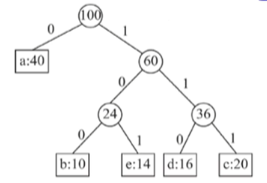
| a | b | c | d | e |
|---|---|---|---|---|
| 0 | 100 | 111 | 110 | 101 |
- 哈夫曼编码所需长度:1x40 + 3x10 + 3x20 + 3x16 + 3x14 = 220
- 等长编码所需长度:3x(40+10+20+16+14) = 300 (五个字符,等长编码,就需要3个二进制位代表一个值。)
压缩比: = ≈ 0.27
13.18 线索二叉树定义【应该是了解即可】
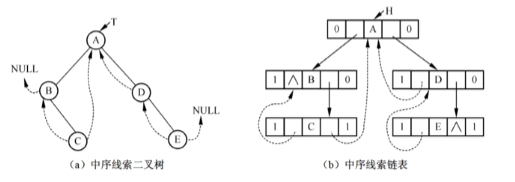
13.19 二叉树类别
- 满二叉树
- 完全二叉树
- 平衡二叉树
- 排序二叉树
- 最优二叉树
十四、图相关
14.1 图形结构与图的定义
图中,任意两个结点之间都可能存在直接关系。所以,图中一个结点的前驱结点和后继结点的数目是没有限制的。
图G是有集合V和E狗策划给你的二元组,记作G=(V,E)。
V是图中顶点的非空有限集合,E是图中边的有限集合。
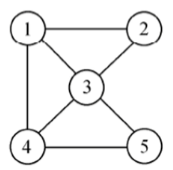
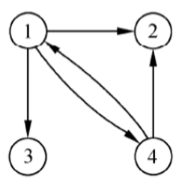
14.2 有向图和无向图
有向图:图中每条边都是有方向的,顶点的关系用<Vi,Vj>表示,Vi到Vj有一条有向边,Vi是起点称为弧尾,Vj是终点称为弧头
无向图:每条边都是没方向的。顶点的关系用<Vi,Vj>表示,但是没有方向上的区别。
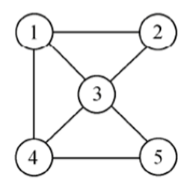
14.3 完全图
无向完全图:无向图若有n个顶点,每个顶点与其他n-1个顶点之间都有边。共有条边。
有向完全图:有向图中,任意来个那个不同的顶点,都有方向相反的两条弧存在。共有n(n-1)条边。
14.4 顶点的度
度:仅无向图存在。当前结点存在的弧的个数。
出度:仅有向图存在。从当前结点指向其他结点的弧的个数
入度:仅有向图存在。从其他结点指向当前结点的弧的个数
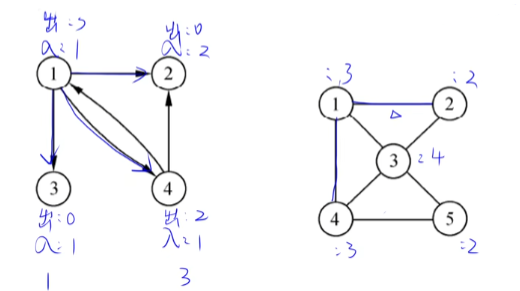
14.5 路径
回路(环):第一个顶点和最后一个顶点相同的路径
简单路径:路径中不包含重复的顶点。若一条路径上除了Vp和Vq可以相同外,其余顶点均不相同。
| 特性 | 简单路径 | 回路(特别是简单回路) |
|---|---|---|
| 起点与终点 | 可以不同 | 必须相同 |
| 顶点是否重复 | 所有顶点都不重复 | 仅起点和终点相同,其余不重复 |
| 是否闭合 | 不闭合 | 闭合 |
🌰****例子:
- 简单路径:A → B → C → D(无重复顶点,起点 ≠ 终点)
- 简单回路:A → B → C → A(起点 = 终点,其余顶点不重复)
14.6 连通图与强连通图
连通图:无向图中任意两个顶点都是联通的。
最少:n-1
最多:
强连通图:有向图中任意两个顶点都有互相联通的路径。
最少:n
最多:n(n-1)
14.7 邻接矩阵
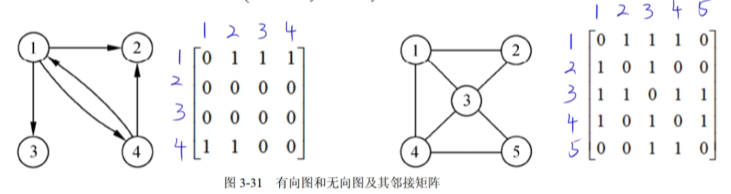
无向图的邻接矩阵是对称的。
无向图:
- 非零元素个数 = e 个
- 顶点Vi的度是邻接矩阵第i行(或列)中值不为0的元素个数
有向图:
- 非零元素个数 = 2e 个
- 第i行(或列)中值不为0的元素个数是顶点Vi的出度
- 第j列中值不为0的元素个数是顶点Vj的入度
14.8 邻接表
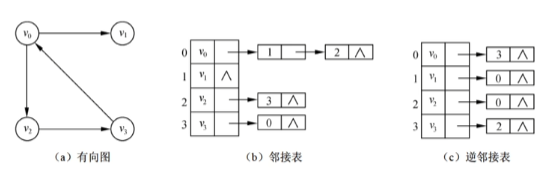
无向图:表节点个数 = e = 邻接矩阵非零元素个数
14.9 稠密图和稀疏图
稀疏图:边的数量 远少于 顶点可能连接的最大边数。(可能图中大部分顶点之间没有直接连接。)
稠密图:边的数量 接近 顶点可能连接的最大边数。(可能图中大部分顶点之间都有边相连。)
| 特性 | 稀疏图 | 稠密图 |
|---|---|---|
| 边的数量 | 少 | 多 |
| 连接程度 | 连接稀疏,很多点不相连 | 大部分点都有边相连 |
| 存储方式建议 | 常用邻接表 | 常用邻接矩阵 |
14.10 网
边(或弧)带权值的图称为网。
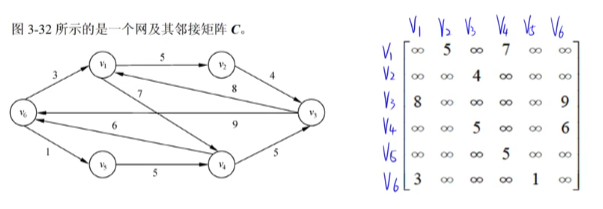
14.11 图的遍历
1 | A |
深度优先算法:
- 定义:从一个起点出发,沿着一条路径尽可能深入地走到底,直到无法继续为止,然后回溯,再尝试其他分支。
- 遍历顺序可能是:A → B → D → C → E → F
广度优先算法:
- 定义:从起点开始,先访问所有距离为1的邻居,再访问距离为2的邻居,逐层向外扩散。
- 遍历顺序可能是:A → B → C → D → E → F
14.12 深度优先遍历
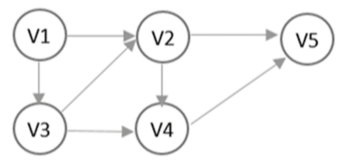
遍历顺序: V1、V2、V5、V4、V3 或 V1、V3、V2、V4、V5
14.13 深度遍历、广度遍历的时间复杂度
深度优先搜索DFS:
- 使用递归的思想进行遍历
- 邻接矩阵时间复杂度:O(n2)
- 邻接表时间复杂度:O(n+e)
广度优先搜索BFS:
- 使用队列的思想进行遍历
- 邻接矩阵时间复杂度:O(n2)
- 邻接表时间复杂度:O(n+e)
14.14 拓扑排序
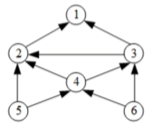
AOV网的特点:
- 顶点:每个顶点代表一个活动。
- 有向边:有向边(A,B)(A,B)表示活动A需要在活动B开始前完成,即A是B的前提条件。
- 无环:为了确保所有活动可以被合理排序并最终完成,AOV网不能包含有向环。如果AOV网中存在环,则意味着某些活动之间存在循环依赖,导致无法进行有效的调度和执行。
AOV网进行拓扑排序:
- 在AOV网选择一个入度为0的顶点,输出它。
- 在网中删除该顶点,以及该顶点有关的所有弧。
- 重复上述步骤,知道网中不存在入度为0的顶点为止。